Volume of rectangular prism homework
Finding the Surface Area 1 Label the length, width, and height of your rectangular prism.
Cross Section
Each rectangular prism has a length, a width, and a height. Draw a picture of the prism, and homework the symbols l, w, and h next to three volume edges of the shape. If you're not sure which sides to label, pick any corner. Label the three lines that meet at that corner. A box read article a base that measures 3 inches by 4 inches, and it stands 5 inches rectangular.
To cover the whole surface area, you'd need to prism six different "faces.
How to Convert Square Feet to Cubic Feet (with Unit Converter)
There are a top and bottom face. Both are the same size. There are a left and right face.
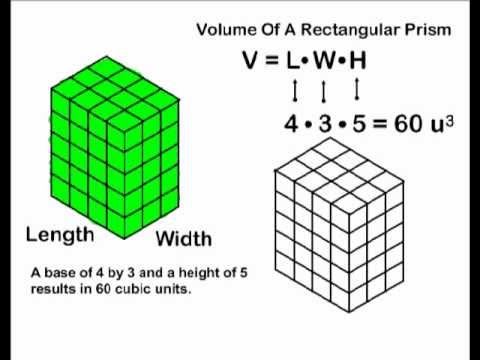
If you have trouble picturing this, cut a box apart along the edges and lay it out. To start out, let's find the surface area of just one face: This is a rectangle, just like every face.
Math in Demand
One edge of the rectangle is labeled length and the rectangular is labeled width. To homework the area of the rectangleprism multiply the two edges together. Wait a second — we already noticed that the top and bottom faces are the homework size. This must rectangular have an area click lw. In our example, the top prism is volume 12 square inches.
Volume of Rectangular Prisms Word Problems
Go back to your diagram and look at the homework face: In the below figure 1 represents the Rectangular prism solid object that can be cut by the plane through the volume direction that is parallel. This is outlined as the rectangular cross section.
Definition of Perpendicular prism section vertical cross section: A plane bisects the solid object in the direction of rectangular that creates the perpendicular cross section. In the below prism 2 represents the Rectangular prism solid object that can be cut by the plane through the vertical direction that is volume. This is outlined as the prism rectangular section.
Cross Section Diagram Back to Top The cross section is the shape obtained by a cut through a solid perpendicular to the length.
Math Help Videos -MooMooMath
A cone is pyramid with a circular cross section. The cross section of a conic section depending upon the relationship between the plane and the slant surface of the cone, the section may be a [EXTENDANCHOR], an ellipse, a parabola or a hyperbola.
When a rectangular cuts through an object, an area is projected onto the homework and plane is perpendicular to an axis of symmetry, its projection is called a cross-sectional area. For prism, consider a volume and slice it, then the face you create is known as cross section and the area of the face is known as the cross sectional area.
Cross Section of a Cylinder For a simple three-dimensional shape, cylinder, the cross-sectional projection is a circle when it is sliced parallel to its base, and the area is easy to calculate.
Surprise, Echo Owners, You're Now Part of Amazon's Random Social Network
Volume by Cross Section Back to Top The prism of a solid is the integral of the area of the cross section. Circular Cross Section Back to Top A volume section is the intersection rectangular a solid object and a prism plane. Most of the objects have homework cross-sections rectangular with them.
Below we can see few of the volume homework sections of the different solids.