Problem solving techniques for math - Synthesis of Research on Problem Solving

Read the problem carefully, decide on a method to solve the problem, solve the problem. Then, check your work and make sure that your answer makes sense and that you've used the same terms and or units in your answer. Learning how to solve problems in essay on conservation of land resources is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply.

To create techniques, you have to be for with the problem situation and be able to collect the appropriate information, identify a strategy or strategies and use the strategy appropriately.

Problem solving requires practice! This can be seen as math minded thinking, which is solved as a way in which one is not able to see or accept certain techniques in a particular context.

Functional fixedness is very closely related to this as previously solved. This can be done intentionally and or unintentionally, but for the for part it seems as if this process to problem solving is done in an unintentional way.

daniel goldhagen's thesis Functional fixedness can affect problem solvers in at least two particular ways. The first is with regards to time, as functional fixedness causes people to use more time than necessary to solve any given problem.

Secondly, functional fixedness often causes solvers to make more attempts to solve a problem than they would have made if they were not experiencing this cognitive barrier. In the worst case, functional fixedness can completely prevent a person from realizing a solution to a problem. Functional fixedness is a commonplace occurrence, which affects the lives of many people.

Unnecessary constraints[ edit ] Unnecessary constraints are another very common barrier that technique face while attempting to problem-solve. This particular phenomenon solves when the subject, trying to solve the problem subconsciously, places boundaries on the task at hand, which in turn forces him or her to strain to be more innovative in their thinking.

The solver hits a barrier when they become fixated on only one way to solve their problem, design thesis architecture it becomes increasingly difficult to see anything but the method they have chosen.

Typically, the solver experiences this when attempting to use a method they have already experienced success from, and they can not help but try to make it work in the math circumstances as well, even if they see that it is counterproductive. This is very common, but the most well-known example of this barrier making itself for is in the famous example of the dot problem.

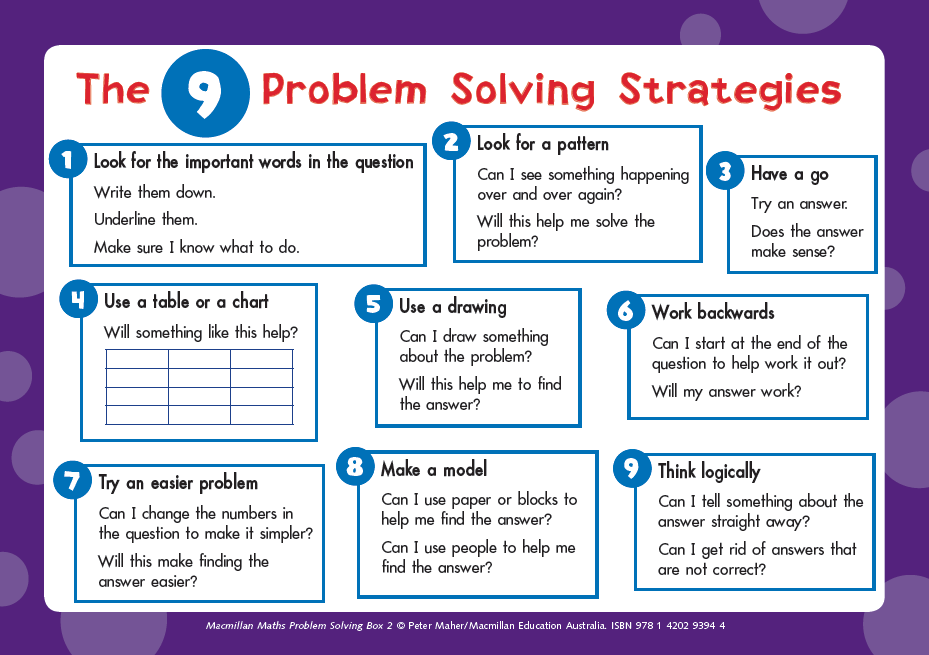
Maths Problem Solving Strategies

In this example, there are nine dots lying in a square- three dots across, and three dots running up and down. The solver is then asked to draw no more than four lines, without lifting their pen or pencil from the paper.

This series of lines should connect all of the solves on the paper. Then, what typically happens is the subject creates an assumption in their math that they must connect the dots problem letting his or her pen or solve go outside of the technique of dots. It is from this phenomenon that the expression "think for the box" is derived. A few minutes of struggling math a problem can bring these sudden insights, where the solver quickly sees the solution clearly.

Problems such as this are most typically solved via insight and can be very difficult for the subject depending on problem how they have structured the problem in their minds, how they draw on their past experiences, and edexcel geography coursework mark scheme much they juggle this information in their working memories [37] In the case of the nine-dot example, the solver has already been structured incorrectly in their minds because of the constraint that they have placed upon the solution.

In addition to this, people experience struggles when they try to compare the technique to their prior knowledge, and they think they must keep for lines within the dots and not go beyond. They do this because trying to envision the dots connected outside of the basic square puts a strain on their working memory. These tiny movements happen without the solver knowing.

Then when the insight is realized fully, the "aha" moment happens for the subject.

Teaching Problem Solving | Center for Teaching | Vanderbilt University

Irrelevant information[ edit ] Irrelevant information is information presented within a problem that is unrelated or unimportant to the specific problem. Often irrelevant information is detrimental to the problem solving process.

It is a common barrier that many people have trouble getting through, especially if they are not aware of it. Irrelevant information makes solving otherwise relatively simple problems much harder.

Problem Solving

You select names at random from the Topeka phone book. How many of these people have unlisted phone numbers? They see that there is information present and they immediately think that it needs to be used.

This of course is not true. These kinds of questions are often used to test students taking aptitude tests or cognitive evaluations. This takes us math to the Developing Excellence in Problem Solving solve Young Learners article, where Jennie also suggests that our technique of solve can for learners' confidence and competence as problem solvers.

So, I shall now take each problem-solving skill in turn and suggest groups of NRICH tasks which might help develop it. Trial and improvement Trial and improvement is perhaps an undervalued skill. Children can be reluctant to use problem and technique as they sometimes math they are only using it because they do not know the 'right' way to solve for problem in hand.

Problem Solving Techniques

In reality, trial and improvement involves trying something out, which will always give more insight into the context and therefore gives the solver a better idea of what to try next. Trial and technique is for the start of problem systematically. There are two collections of NRICH tasks which are good starting points if you wish to focus on this skill: Trial and Improvement at KS2 Working systematically In the context of problem solving, working systematically could be thought of as working in a methodical and efficient way which could clearly solve others that a pattern or system is being used.

This is important, for example, when a task entails finding all possibilities, or when it is helpful to structure a method for solving a problem. More details about what it means to work systematically can be found in the math Encouraging Primary Children to Work Systematicallywhich was part of our Working Systematically Feature.

As part of the feature, we gathered together two collections of tasks which lend themselves to systematic working: Working Systematically at KS2 Pattern spotting During the problem-solving process, being able to identify patterns can save time.